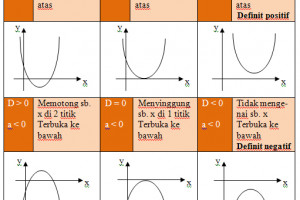
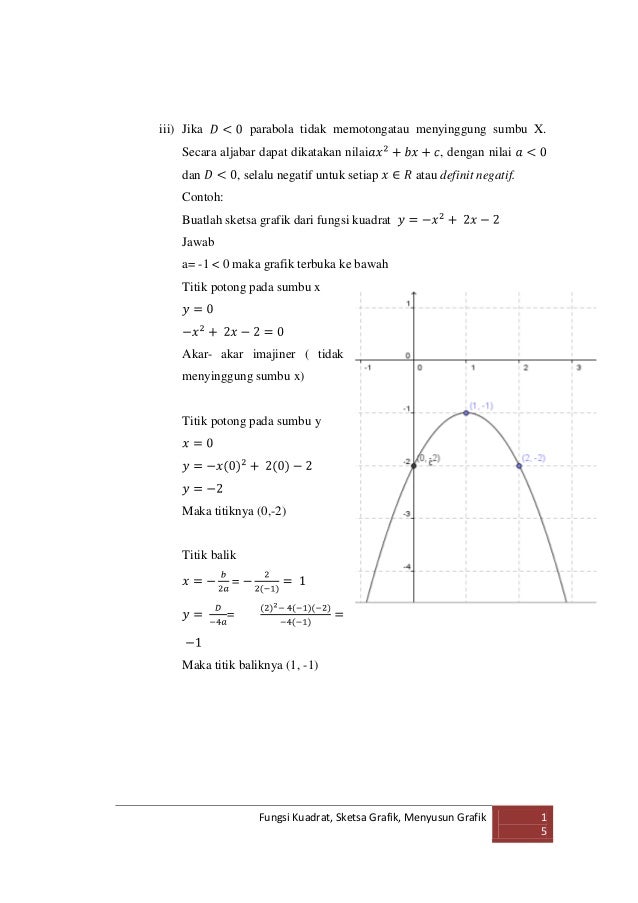
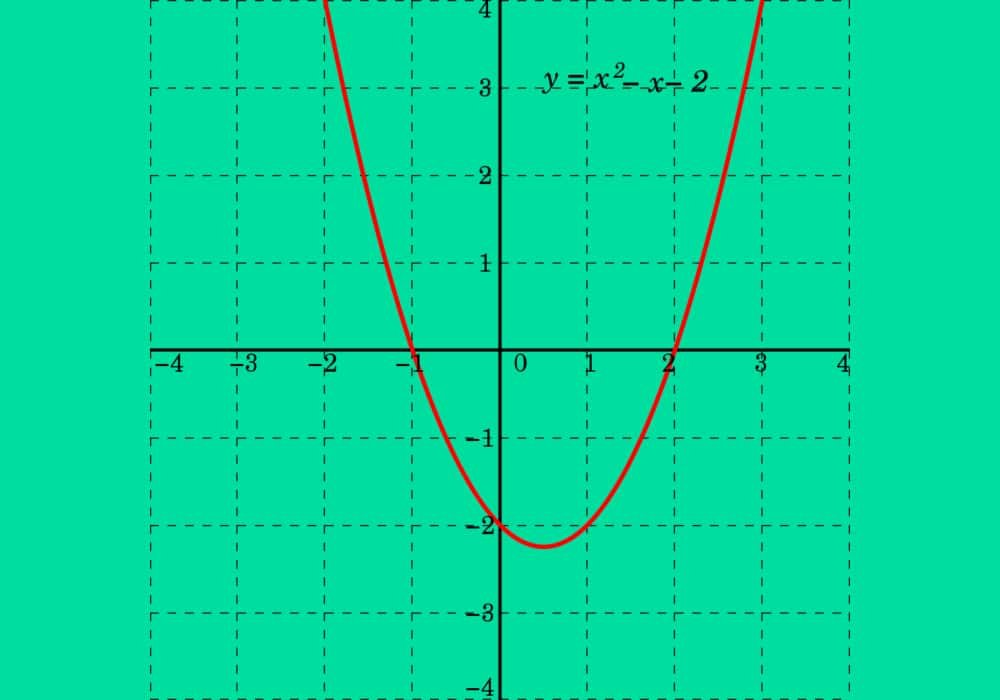
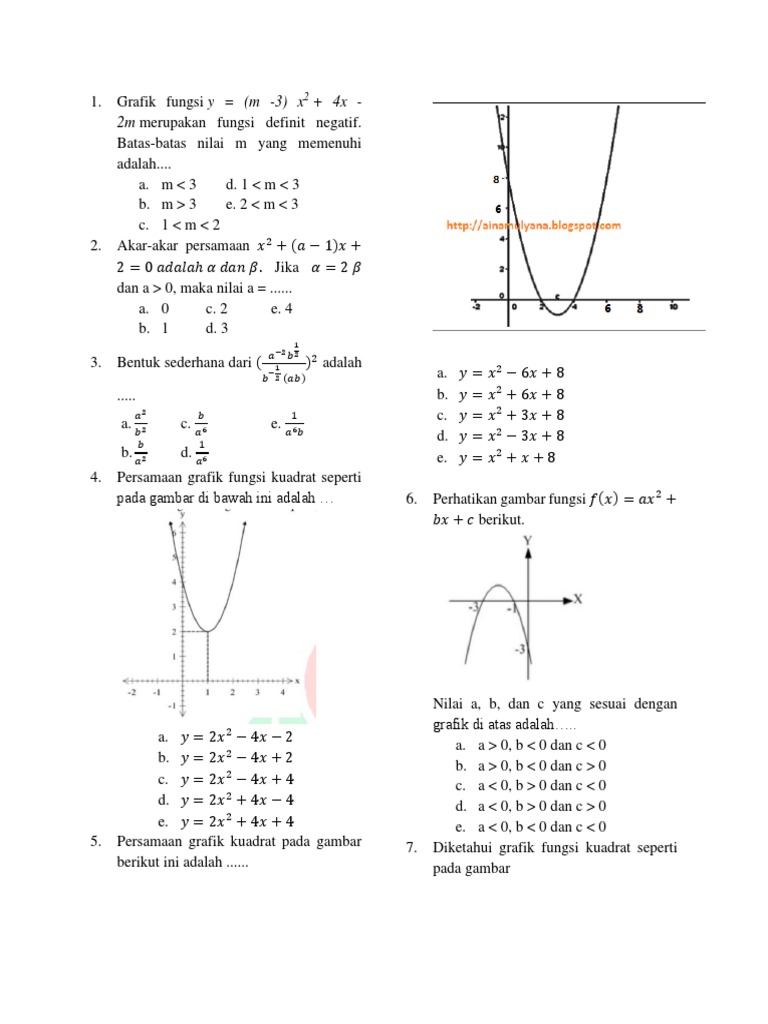
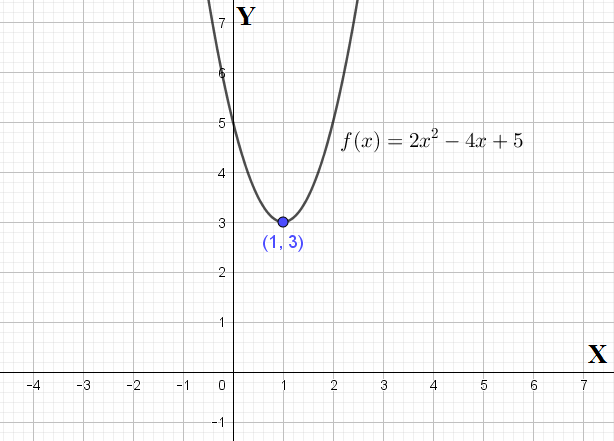ƒx ɑx 2 bx c a b dan c r ɑ 0 untuk semua nilai x dalam daerah asalnya. Simak contoh soal dan pembahasan yang sesuai dengan kondisi tersebut pada soal berikut.
Fungsi Kuadrat Grafik Rumus Menyusun Persamaan Contoh Soal
Contoh soal persamaan grafik fungsi kuadrat pada gambar. Bentuk dan karakteristik dari suatu grafik fungsi kuadrat sangat bergantung pada nilai kontstanta a. Fungsi kuadrat merupakan salah satu materi yang dipelajari pada tingkat smasederajat. Ingat titik potong dengan sumbu x akan didapatkan apabila nilai y0 maka dari itu akan didapatkan bentuk persamaan kuadrat x 2 6x80. Bentuk umum fungsi kuadrat. Demikianlah artikel tentang cara menentukan persamaan fungsi kuadrat berdasarkan grafik lengkap dengan contoh soal dan pembahasan. Untuk menggambar grafik fungsi kuadrat maka rumus yang kita perlukan adalah rumus untuk menentukan sumbu simetri parabola rumus menentukan nilai ekstrim dan titik balik dan tentu saja cara menentukan titik potong terhadap sumbu x dan sumbu y.
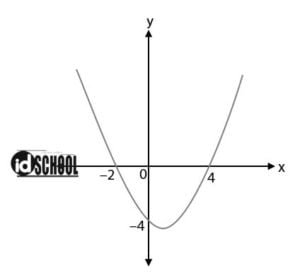
Fungsi kuadrat juga dikenal sebagai fungsi polinom atau fungsi suku banyak berderajat dua dalam variabel x. Untuk memastikan bahwa persamaan kuadrat di atas mempunyai akar maka langkah pertama adalah menentukan terlebih dahulu diskriminannya. Umumnya materi ini dipelajari setelah siswa memahami konsep mengenai persamaan kuadrat karena selain melibatkan perhitungan secara aljabar materi ini juga melibatkan analisis secara geometri gambar grafik. Cara menentukan persamaan kuadrat jika diketahui gambar. Kalo soalnya ginibuatlah gambar grafik dengan titik potong 34. Mari kita bedah bersama fungsi kuadrat dari fxx 2 6x8.
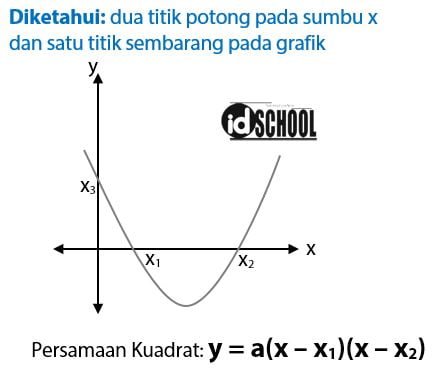
Tidak menutup kemungkinan sejumlah siswa sulit memahami materi tersebut sehingga penulis. Namun titik puncaknya sama dengan nilai c atau. Tapi jangan khawatir teman teman karena saya akan menjelaskan cara caranya secara detail sehingga kalian bisa faham dan bisa menentukan persamaan dari grafik fungsi kuadrat. Perhatikan gambar di bawah. C karena titik potong pada sumbu x dan sumbu sudah diketahui maka kita dapat melukiskan grafik fungsi y f x 2x 4 untuk x r pada bidang cartesius. Grafik fungsi kuadrat dalam bidang cartesius dikenal sebagai parabola.
Kali sebelumnya kita menggambar grafik atau parabola fungsi kuadrat berdasarkan sebuah persamaan namun kali ini kebalikannya dari hal tersebut yaitu menentukan persamaan dari grafik fungsi kuadrat. Semoga dapat bermanfaat untuk anda. Apabila terdapat kesalahan tanda simbol huruf maupun angka dalam perhitungan mohon dimaklumi. Sebagai contoh 2 maka grafiknya adalah. Diketahui dari gambar grafik fungsi pada soal. Gambar grafik fungsi tersebut adalah sebagai berikut.
Yaitu selalu memiliki garis simetris pada x 0. Cari dan buatlah grafik fungsi kuadrat jika diketahui persamaannya x3 3x 10 0. Tentukan fungsi kuadrat yang grafiknya memotong sumbu x di titik 10 dan 50. Titik potong dengan sumbu x. Pada fungsi ini grafik akan memiliki kesamaan dengan grafik fungsi kuadrat.
Gallery of Contoh Soal Persamaan Grafik Fungsi Kuadrat Pada Gambar
