Gambar kurva berbentuk lonceng ini sebagai ilustrasi. Buat daftar distribusi kumulatif relatif kurang dari.

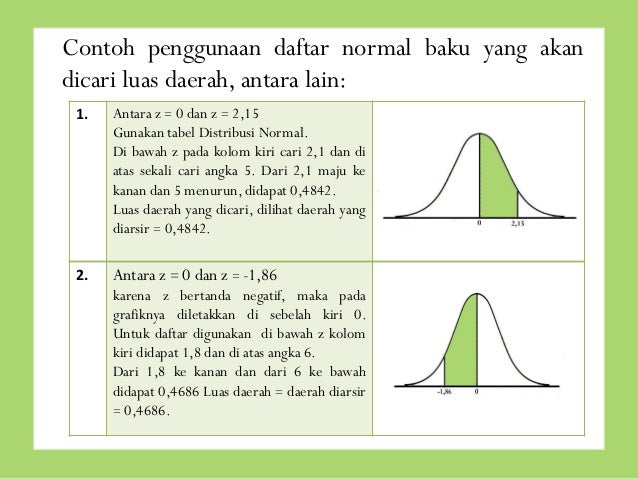
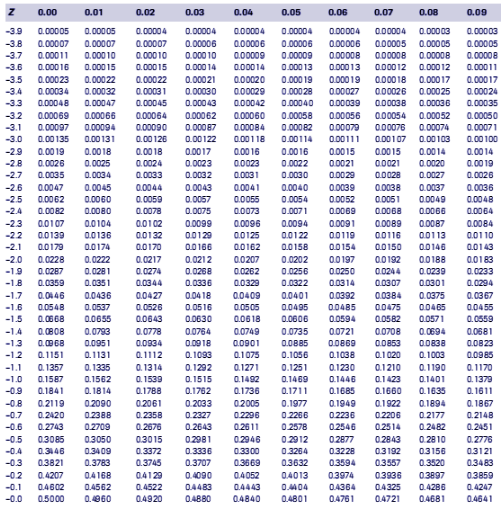
Menghitung Luas Area Dengan Menggunakan Tabel Z Distribusi
Contoh distribusi normal statistik. Berapa peluang alat elektronik tersebut tak akan rusak antara 778 hari dan 834 hari. Tabel distribusi normal memiliki isi peluang dari nilai z atau p z z. Abraham de moivre lah yang memperkenalkan tentang distribusi normal untuk pertama kali di dunia di dalam suatu artikel miliknya pada tahun 1733 sebagai pendekatan distribussi binomial untuk n besar. Berikut ini akan dijelaskan mengenai beberapa contoh penerapan distribusi normal. Distribusi student ini berlaku baik untuk sampel kecil maupun sampel besar. Hubungkan titik titik yang digambarkan di kertas peluang tadi.
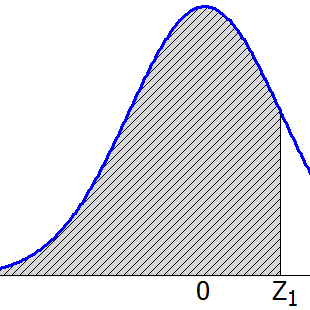
Simpulkan bahwa data berdistribusi normal atau mendekati distribusi normal apabila titik titik yang dihubungkan tersebut merupakan garis lurus atau hampir lurus. Harga saham ke 20 perusahaan tersebut berkisar antara rp. Sebuah alat elektronik diberikan jaminan tak akan rusak rata rata selama 800 hari. Misalkan kita memilih 20 saham pada bulan mei 2007. Baca juga mean median modus. Berdasarkan kurva distribusi normal di atas distribusi normal memiliki rata rata mean sama dengan 0 dan simpangan baku sama dengan 1.
Apabila digambarkan dalam grafik kurva distribusi normal berbentuk seperti genta bell shaped yang simetris. Dengan demikian rata rata aritmetik modus dan median menjadi ukuran yang baik untuk melakukan estimasi. Ketika suatu populasi mengikuti distribusi normal observasi ter klaster di sekitar rata rata aritmetiknya. 2000 2805 per lembarnya. Gambarkan nilai daftar tersebut ke kertas peluang. Distribusi normal merupakan salah satu distribusi probabilitas yang penting dalam analisis statistikadistribusi ini memiliki parameter berupa mean dan simpangan bakudistribusi normal dengan mean 0 dan simpangan baku 1 disebut dengan distribusi normal standar.
Kebanyakan karakter alam dan manusia mengikuti distribusi normal. Rumus diatas distribusi normal tergantung pada 2 parameter yaitu rata rata u x dan varians σ kuadrat xdengan kata lain distribusi normal umum merupakan sekeluarga kurva yang berparameter dua buah dan agar kita memperoleh suatu gambaran tentang distribusi normal yang khusus kedua parameter diatas harus diberi harga yang tertentu pula. Pada n 30 distribusi t ini mendekati distribusi normal dan pada n yang sangat besar misalnya n10000 nilai distribusi t sama persis dengan nilai distribusi normal lihat tabel t pada df 10000 dan bandingkan dengan nilai z. Contoh soal distribusi normal iii 3. Distribusi ini merupakan distribussi yang paling penting dan paling banyak digunakan di bidang statistika. Distribusi normal merupakan distribusi yang paling banyak dipakai.
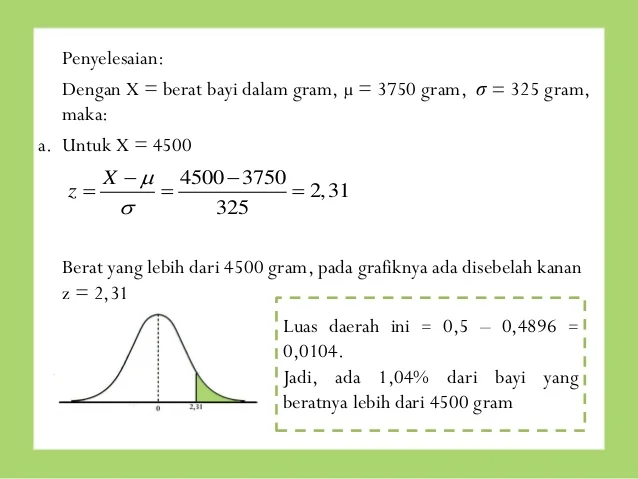
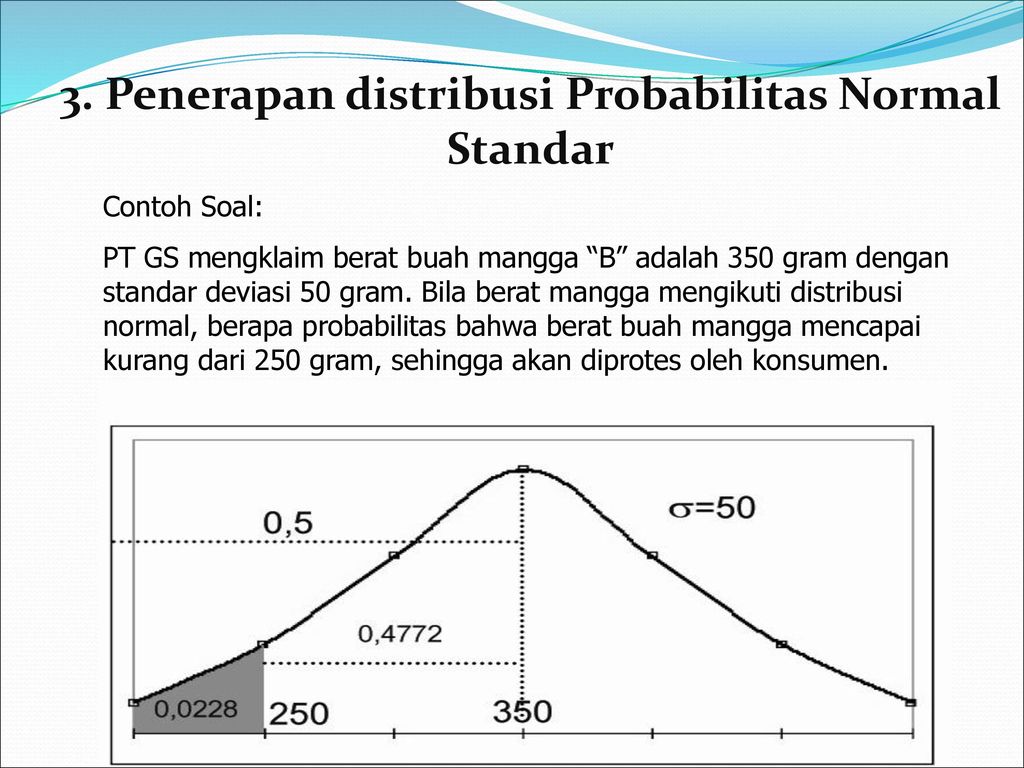
Banyak masalah yang dapat diselesaikan memakai jasa distribusi normal seperti beberapa contoh berikut. Sebagaimana diketahui bahwa nilai peluang selalu ada di antara 0 dan 1 sampai nilai di dalam tabel ada diantara 0 dan 1. Biasanya juga distribusi normal sering dinamakan sebagai pengertian distribusi gauss. Dengan standar deviasi 40 hari.